[二更] 上次很辛苦的更完了為啥義大利麵不隻斷成兩段的硬核物理解釋，然後又發現有人做了個視頻，用每秒1百萬幅的高速相機捕捉義大利麵斷裂的瞬間。這個視頻基本get到了文章理論部分的幾個關鍵點。看公式頭大的話就看下面的視頻吧。
為啥義大利麵總斷成好幾段？https://www.zhihu.com/video/1225622976890413056
[更] 沒想到真的有不少朋友對這種沙雕問題感興趣，那我就更嘍。先感謝那些點贊關注評論催更的朋友們！
評論區也有朋友指出有人發過這個關於義大利麵的了，我也看了那個文章，應該是全文翻譯的MIT的新聞稿。我本人是很喜歡那個文章的。但如果你不小心看過我這個專欄置頂的文章，你會發現我的側重點是介紹這些看似沙雕的研究背後的硬核物理。看新聞稿肯定是輕松愉悅的，但那是別人咀嚼過的，真正有營養的東西的在原文獻裡面。
我們知其然，還要知其所以然。
這個文章可能要長文預警，介紹學術文獻也不可避免地會出現公式和專業術語。當然，我深知斯蒂芬.霍金說過的真理：一個公式能嚇跑一半讀者！不過不要害怕，看不懂的地方略過也不會影響理解。【中括號內的都可以直接略過】。
以下：
本文打算介紹下2006年搞笑諾貝爾獎物理學獎。
為什麼幹義大利麵折斷的時候，總是多於兩段？
獲獎文章發表於 Physical Review Letters 95，095505 (2005).
這個問題曾經讓正牌諾貝爾物理學獎得主理查德.費曼非常的困擾。據說他花了幾個小時在廚房裡掰幹義大利麵，就為了搞清楚為什麼義大利麵總是斷成好幾段，而不隻是兩段？當然他的廚房實驗失敗了。更令他沮喪的是他也沒有找到為啥義大利麵總是斷成好幾段的合理解釋。最終他也沒能活著看到上面那篇文章的發表。
這個問題描述的是桿狀物質的級聯斷裂現象。義大利麵隻是其中一個例子。
2012年奧運會撐桿跳的比賽現場就發生了類似的一幕：
撐桿跳運動員展示級聯斷裂https://www.zhihu.com/video/1224648915255267328
2005年的PRL文章給出了理論解釋。
另外，2018年發表在美國科學院院刊PNAS上的一篇文章，來自MIT的科學家們則展示了如何控制義大利麵的斷裂，成功的將義大利麵折成兩段！
動圖來源：http://news.mit.edu/2018/mit-mathematicians-solve-age-old-spaghetti-mystery-0813
動圖來源：http://news.mit.edu/2018/mit-mathematicians-solve-age-old-spaghetti-mystery-0813
先賣個關子，這麼沙雕的問題，有人關注的話再更吧！
有很多人催更，鞠躬、感謝！
以下內容大概會分成兩部分：先介紹2006年搞笑諾獎的那篇PRL，理論解釋為啥幹義大利麵總是斷成好幾段？若是大家還感興趣的話，請留言，我再介紹2018年那篇PNAS，如何成功的將義大利麵折成僅僅兩段？
OK， 那篇PRL[1]來自法國巴黎第六大學的Basile Audoly和Sebastien Neukirch。
先上結論：
波，彎曲震動波《flexural waves》。
當一根彎曲的義大利麵被突然釋放，義大利麵兩端的曲率在很短的時間內(微秒)迅速改變為零，激發震動波。震動波局域性的增加義大利麵的曲率。當一個位置的曲率高於一定值後斷裂發生。 斷點位置的曲率迅速變化又激發新的震動波，導致更多的斷裂出現，如雪崩過程。 結論似乎很簡單，評論區很多朋友也都猜的八九不離十了。我們來看結論是怎麼來的。
首先建立模型。我們考慮兩端都被固定《或用手拿著》的義大利麵，不斷的用力使其慢慢彎曲以增大其曲率。當你把它掰斷的那個瞬間我們記為初始狀態 t=0 ，這個狀態下義大利麵的曲率 \kappa_0 達到某一個閾值記為 \kappa^{*} 。需要強調的是，在這個瞬間，第一個斷裂發生，因此僅有兩段義大利麵，他們的一端仍然被固定《比如還在你手上》，另一端因為斷裂發生而被釋放。瞬時狀態可由下圖1表示。
因為我們研究的是級聯斷裂過程，必然先會有初始的第一個斷裂。但是我們不再討論這個初始斷裂是怎麼發生的了，而將重點放在任意一半義大利麵後續的動力學過程。闡述 t>0 的後續動力學過程如何導致新的斷裂的發生。
圖1，第一個斷裂發生以後的義大利麵模型。圖片來自[1].
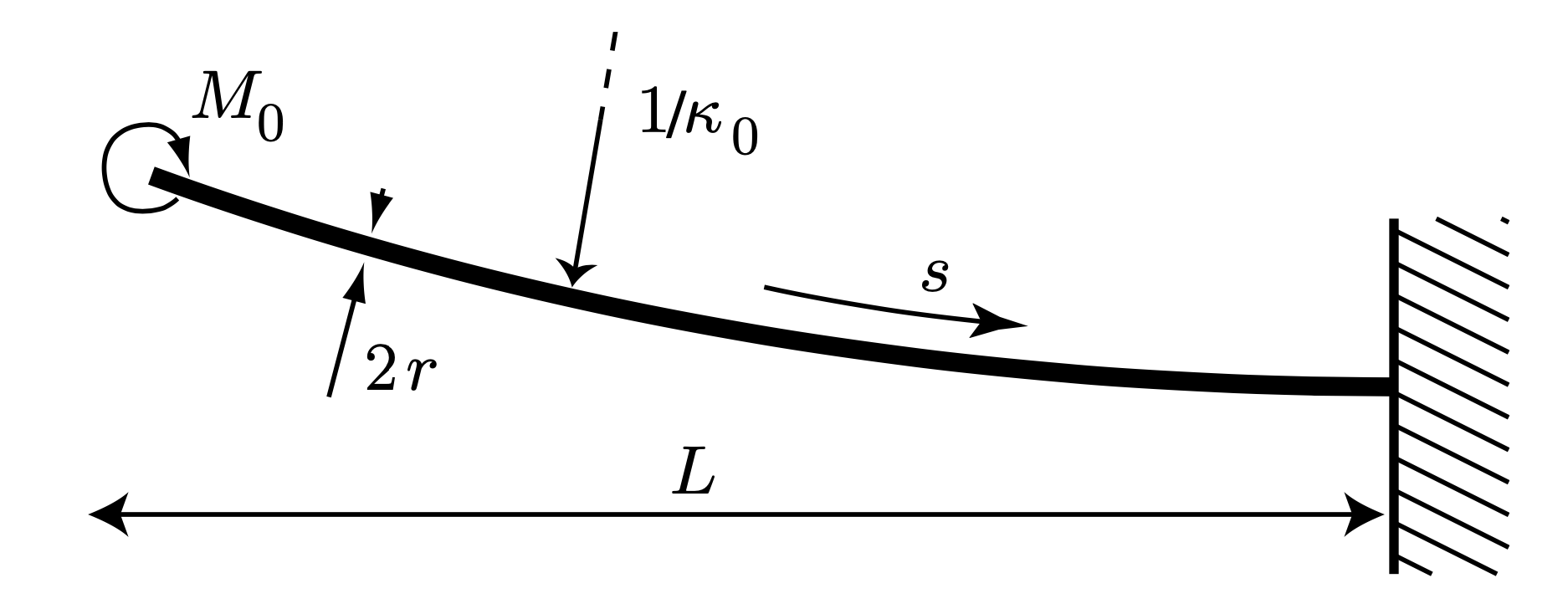
圖1的模型模仿斷裂發生的瞬時狀態，義大利麵一端固定在墻上，另一端被施加力矩 M_0 因而呈現出彎曲狀態。顯然，這一端的力矩被釋放的過程等效於斷裂發生的過程。因此這樣一個模型能夠模擬初始時掰斷的兩段義大利麵其中一段。
在 t=0 時釋放義大利麵， 力矩M_0 瞬間消失，原來的平衡態被打破。隨後的動力學過程可由著名的基爾霍夫方程描述:【 L^4\kappa_{,s^4}(s,t) + T^2\kappa_{,t^2}(s,t) = 0， 這裡 s 為弧長坐標，逗號代表偏導。 T = L^2/\gamma 表征義大利麵柱狀體的力學性質， \gamma = \sqrt{EI/\rho A} ， E 為楊氏模量， \rho 為密度， A 為橫截面積， I 為截面的轉動慣量。這裡的 T 正比於義大利麵材料固有震蕩周期 T_{free} = 1.79T 。】
對這個動力學方程有兩點說明：1》線性假設，隻考慮非常小的偏移。2》僅考慮圖1平面內義大利麵的變化過程。 有了動力學方程，求解 \kappa(s,t) 的話要先找初始條件和邊界條件。【很顯然兩個邊界，墻上固定的一端和自由端。固定端 s=L 處滿足 \kappa_{,s^2}(L,t)=0 ，\kappa_{,s^3}(L,t)=0；自由端 s=0 處滿足 \kappa(0，t) = 0 ，\kappa_{,s}(0,t)=0。 初始條件也有兩個，最初在 s=0 處的曲率已知 \kappa(s,0) = \kappa_0，以及初始時靜止沒有初速度，即初始曲率對時間的偏導為零 \kappa_{,t}(s,0) = 0 。】六個限制條件理論上能唯一的確定動力學方程的解 \kappa(s,t) 。
但是，不知道大家有沒有注意到邊界條件和初始條件存在不自洽的地方。因為自由端的邊界條件要求s=0 處的曲率為零(所以叫『自由』)，但是初始條件告訴我們了那一端的曲率在 t=0 時為 \kappa_0 \ne 0 。這個不自恰的地方可以這樣理解：義大利麵的曲率正比於其內部力矩，在自由端力矩為零則曲率也應為零；這與我們最初認為的整個義大利麵初始時各點的都具有相同的非零曲率不符。這是因為存在一個典型的邊界層。厚度約為 r 的邊界層對應一個特殊的時間尺度 T_s = r/c \approx 1 ~ \mu s ，其中 c 為橫向斷裂在義大利麵內部傳播的典型速度。這個1微秒的時間尺度相比於我們研究的級聯斷裂的時間尺度是很小的， T_s / T = 0.5 (r/L)^2 \sim 0.0001 。
換句話說，自由端邊界附近的初始曲率 \kappa_0 在 T_s 的極短時間內恢復為零。這個彎曲狀態突然被釋放的過程造成一個突發的彎曲震動波。注意在時間尺度上 T_s 很短，而固有時間 T 很長，因此我們研究的過程的時間尺度滿足 T_s \ll t \ll T 可稱為中間漸近態。這樣的情形下上面的動力學方程是可以獲得解析解的。
具體的求解過程我還是略過吧，直接給出解的形式：
【 \kappa(s,t) = 2\kappa_0S(\frac{1}{\sqrt{2\pi}}\frac{s}{\sqrt{\gamma t}}) 】
這個解裡面的 S 為菲涅爾正弦積分。學過波動光學的一定知道近場菲涅爾衍射是什麼樣子的。
從這個解裡面能得出重要結論：這個解描述的並非是速度恒定(s \sim ct)的漸進波，而是自相似(s\sim\sqrt{\gamma t} )的解。 這種中間態的自相似通解不依賴材料的特性，不依賴初始的斷裂過程，甚至不依賴固定一端的邊界條件《實際上這個解的求解過程並沒有用到 s = L 處的邊界條件，關於自相似的概念請參考維基百科》。
下圖2b直觀的畫出了這個解析通解隨自相似參數 \xi = (s/L)/\sqrt{t/T} = s/\sqrt{\gamma t} 的變化規律。圖2a則給出了數值解的圖像。這個圖像成功的捕獲了上面討論的幾個重要的地方：首先，自由端 s=0 位置處的曲率 \kappa(0,t) 在幾個數值計算步長內迅速減弱為零；其次，從自由端發出的震動波的速度隨 \sqrt{t} 變化；最後，在 t\sim T 震動波被邊界反射回來之前，都具有自相似的形式。
圖2，a基爾霍夫方程的數值解，b自相似解析解。圖片來自[1]。
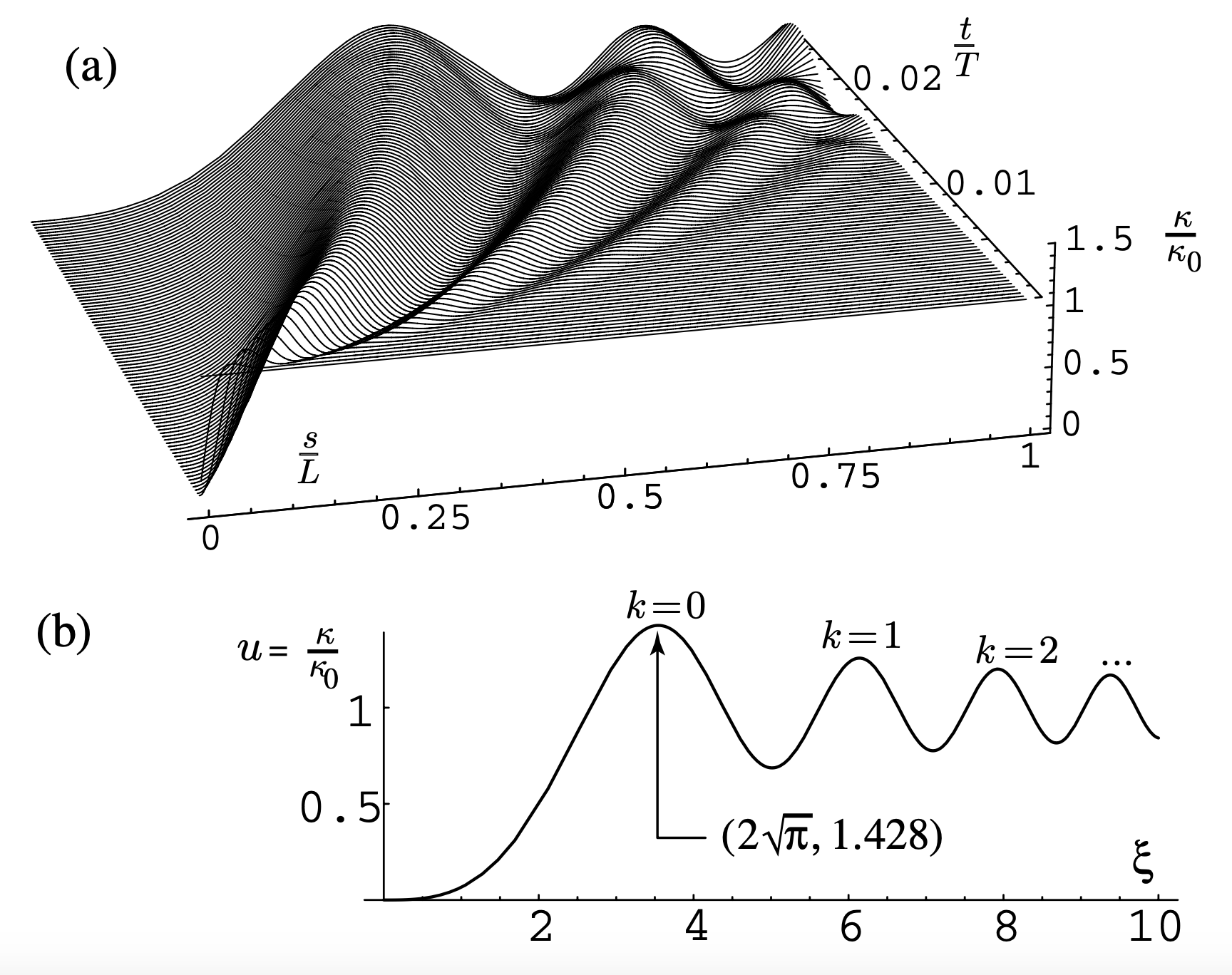
這個自相似解的一個關鍵性質為彎曲義大利麵的局域曲率可以很大程度上超過最初的極限斷裂曲率 \kappa_0 。例如圖2b在自相似參數為 2\sqrt{\pi} 處的曲率為1.428倍的初始曲率。這個系數是普適的，2倍於菲涅爾正弦積分的最大值。
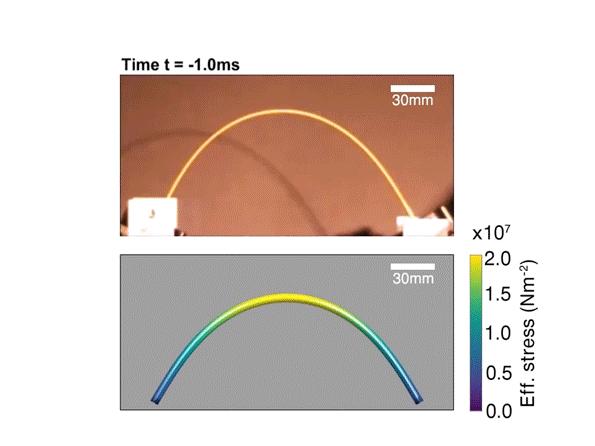
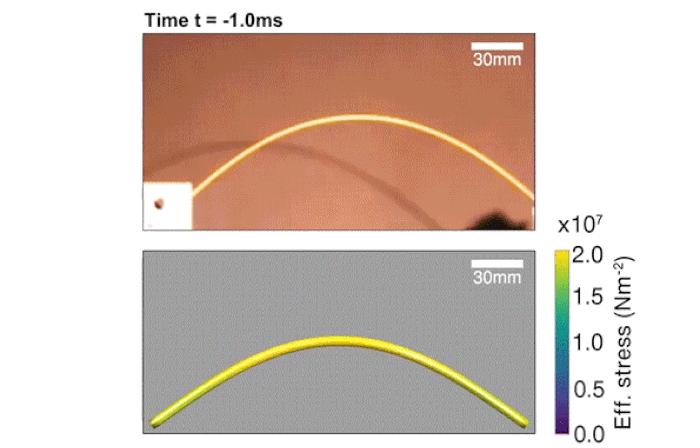
這個理論預測的曲率增大得到了實驗驗證，如圖3所示。
圖3，簡單的義大利麵彎折實驗。義大利麵一端被釋放，另一端被固定。義大利麵的快速變化由幀幅率每秒1000張的高速相機采集。圖片來源[1]。
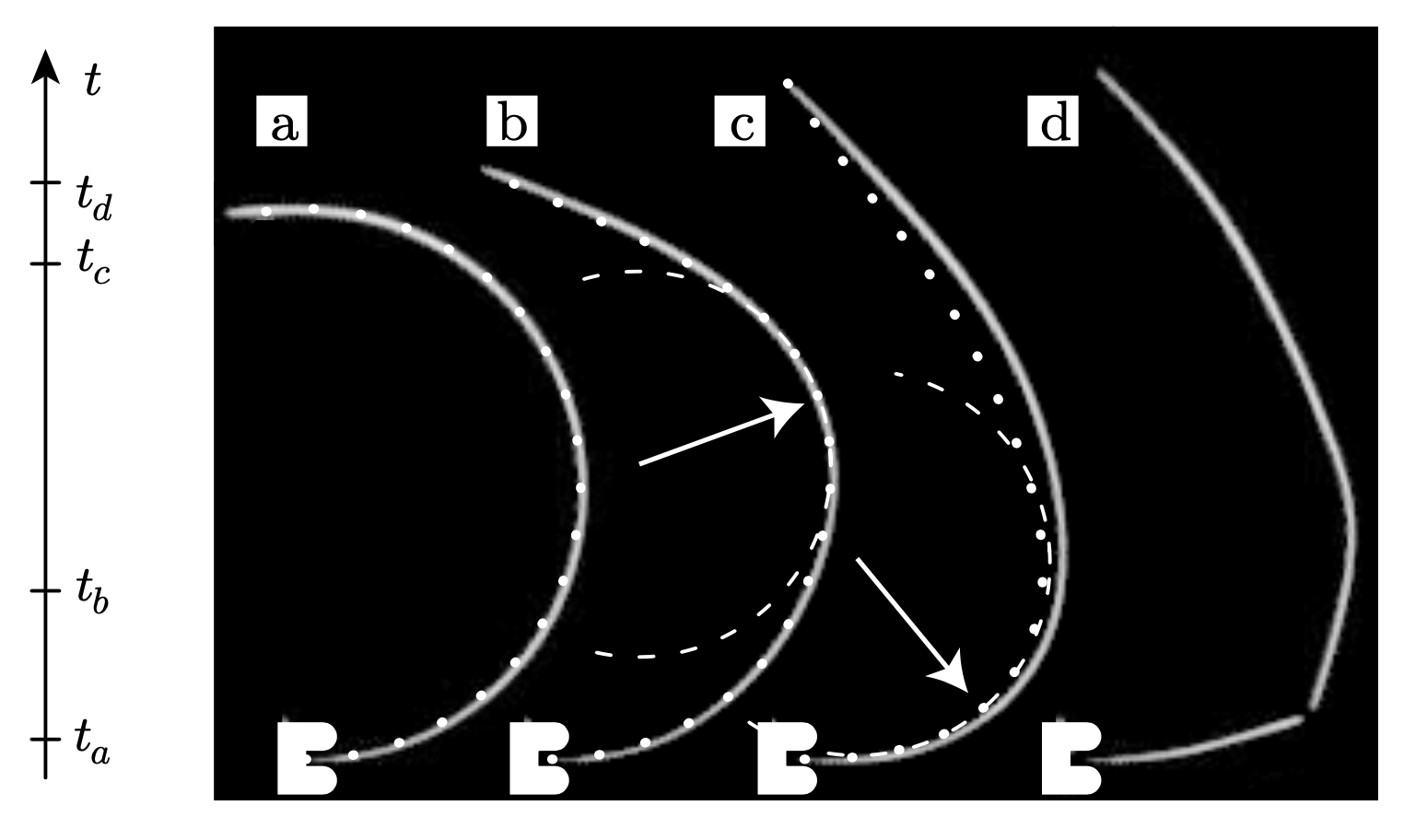
實驗中采用的是Barilla 1號義大利麵，長度為24.1厘米。義大利麵被彎折成 195^\circ 《圖3a》。為了捕獲義大利麵的快速變化過程，用來拍照的相機幀幅率為每秒1000幅。一端釋放以後的中間態《b,c》可以看出震動波的產生，表現為義大利麵局域曲率的變化。圖3中點劃線代表的是數值模擬預測的義大利麵形狀，虛線代表的是最大曲率位置處的內切圓。很明顯可以看出，b和c中中間態的最大曲率超過初始的曲率(對應的自然是曲率半徑的減小)。c對應的是一端釋放後第一個斷裂將要發生的時刻。這時，自相似系數和最大曲率位置都跟上面的解析解預測的一致：最大曲率點在 s=0.76L 處，對應的曲率半徑為 1/(1.428\kappa_0) 。d時刻為緊隨c以後的斷裂發生的時刻。我們也可以清楚的看到，斷裂以後新的義大利麵自由端的曲率迅速變為零《平直的義大利麵》，而新的震動波又得以產生。
這樣，這一段義大利麵又一分為二了，加上初始斷裂時的另一段我們已經至少有三段了。其實只要新的震動波的強度足夠，還會有更多的斷裂。
【本人剛剛在廚房試了下，屢試不爽，總是很輕松的把義大利麵掰的稀碎。】
文章最後一部分我就一筆帶過了《否則看的人就越來越少了吧？》
最後改變不同型號《不同材質和半徑》的義大利麵，以及改變初始的曲率來重復圖3的實驗。結論是：斷裂的發生對初始曲率非常敏感；在空間-時間相圖(s/L，t/T )上所有的斷裂都集中在某些特定的區域《這是自相似性的體現》。
以上大概就是為啥義大利麵總是斷成多於兩段的理論解釋了。 理論好像總是有點枯燥。
不過MIT的PNAS工作[2]就有意思的多了。折成僅兩段的方法評論區的部分朋友已經猜出來一半了，(有的人就是很聰明！)
至於到底是什麼方法？又是為什麼？
您要是還有興趣，請移步這裡：
[走之前別忘左下角 \Downarrow ]